
1. 최소신장트리(Minimum Spanning Tree)의 이해
"신장트리"(이하 Spanning Tree)란, 1. 그래프의 형태를 취하면서, 2. 모든 노드들이 연결되어 있고, 3. 트리의 조건을 충족하여 사이클이 존재하지 않는 자료구조이다. 아래의 그림은 일반적인 그래프(좌)와 신장트리(우)의 예를 나타내고 있다.

앞서 Spanning Tree는 모든 노드들이 연결되어 있고, 사이클을 갖지않는 그래프라고 언급했는데, 그 중 모든 간선(edge) value의 합이 최소를 띄는 Spanning Tree가 MST(최소신장트리)이다.

간선의 가중치가 존재하는 그래프에서 MST를 찾는 과정(알고리즘)의 대표적인 예가 크루스칼 알고리즘(Kruskal's algorithm)과 프림 알고리즘(Prim's algorithm)이다.
2. 크루스칼 알고리즘(Kruskal's Algorithm)
그래프에서 탐욕 알고리즘을 활용하여 MST를 찾는 concept의 알고리즘이다. 좀 더 친절하게 설명해볼까. 앞선 포스팅에서 탐욕 알고리즘이란 '눈 앞의 이익을 우선하여 선택하여 최적의 해와 근사한 해를 빠르게 찾는 알고리즘'이라고 설명했는데 (탐욕 알고리즘이 궁금하면 클릭), 이를 활용하여 눈 앞의 가장 작은 간선의 값을 갖는 노드를 우선 연결해가며 MST를 찾아간다.
하나의 그래프에서 다수의 MST가 존재할 수 있다. 크루스칼 알고리즘은 가장 빠르게 MST 하나를 찾는 것에 목표를 둔다. 한붓그리기가 하고 싶거나 존재할 수 있는 모든 MST를 찾아야 한다면 뒤에서 배울 프림 알고리즘이 활용하기엔 좀 더 적합할 것이다.
2.1 Kruskal's Algorithm의 과정
1) 모든 정점을 각각의 집합으로 초기화한다.
2) 모든 간선을 가중치를 기준으로 sorting하고, 최저 값을 갖는 간선의 양 노드부터 비교한다.
3) 두 노드(정점)의 루트 노드를 확인하고, 다를 경우 연결한다.
- 두 정점을 연결시킬경우, 어떤 노드를 루트로 설정할 것인가. -> 루트노드는 결국 상관없음. 둘 중 아무거나 루트로 만들면 됨.
2.2 "두 노드의 루트 노드를 확인하고, 다를 경우 연결" : Union-Find 알고리즘
- Union-Find Algorithm이란?
두 집합의 교집합이 없는 서로소 집합(Disjoint Set)을 표현할 때 사용하는 트리 구조를 활용한 알고리즘이다. 노드들 중 연결된 노드를 "찾거나", 서로 "연결"할 때 사용한다.
Union시, 순서에 따라서 최악의 경우 아래 그림과 같이 한쪽으로 치우친 트리구조(skewed-BST)가 될 수 있다. 그럴 경우 Find/Union시 성능이 O(N)이 될 수 있으므로, 두 트리를 연결할 때 union-by-rank나 path compression등의 기법이 활용된다.

- union-by-rank 기법: Union을 효율적으로
각 트리에 대해 높이(rank)를 기억하고, union시 두 트리의 rank(높이)에 따라 union을 다르게 수행하는 방식이다.
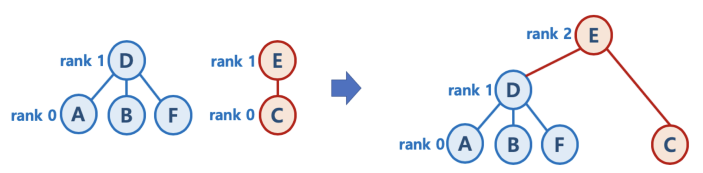
두 트리의 rank가 다르다면, 높이가 큰 트리를 전체 트리의 루트노드가 되게 해서 높이가 작은 트리를 큰 트리를 붙인다.
두 트리의 rank가 같다면, 한 쪽의 트리의 루트노드의 rank를 1증가시켜 앞의 과정을 반복한다.
해당 기법을 사용하게 될 경우, find과정이 소요 시간이 가장 많으며 총 O(logN)의 시간복잡도를 갖게 된다.
def Find(x):
if x.parent == x:
return x;
else
return Find(x.parent);
def Union(nodeV, nodeU):
rootV = Find(nodeV);
rootU = Find(nodeU);
if rootV.rank > rootU.rank:
rootU.parent = rootV;
else:
rootV.parent = rootU;
if rootV.rank == rootU.rank:
rootU.rank += 1;
- path compression(경로 압축) 기법: Find를 효율적으로
Find연산을 수행할 때마다 트리의 구조를 아래와 같이 평평하게 만드는 방식이다. 루트 노드까지 순회할 때 방문한 각 노드들이 부모노드로 직접 루트 노드를 가리키도록 갱신하는 것으로, 하나의 집합에 속한 모든 각 노드들은 같은 부모 노드를 공유하게 된다. 코드는 아래와 같으니 참고하도록 하며, union by rank 기법과 path compression 기법은 상호 보완 적용할 수 있다.
def Find(x):
if x.parent != x:
x.parent = Find(x.parent);
return x.parent;

- 결론적으로,
union-by-rank와 path compression을 활용하게 될 경우 Union과정에서 O(logN)을 M번 반복 적용시키므로 O(Mlog*N) (반복 로그, 로그 스타)의 성능을 보인다. 이는 수학적으로 밑이 2일 경우 5보다 큰 값을 가지지 않으므로 O(1)로 봐도 무방하다.
2.3 Kruskal's Algorithm의 성능
앞서 Kruskal's Algorithm은 아래와 같은 3단계의 과정을 거친다고 말했다.
1. 모든 정점을 독립적인 집합으로 초기화하고, -> O(v) = O(1) /* vertex의 수 만큼 수행 */
2. 모든 간선을 weight를 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다. -> quick sort시, O(ElogE) /* E는 간선 */
3. 두 정점의 최상위 정점을 확인하여, 다를 경우 Union-Find 알고리즘을 통해 두 정점을 연결한다. -> 앞서 O(1)로 봐도 무방하다고 말함
결국 1번과 3번 step은 시간복잡도가 상수에 가까우므로 2번 과정에 의해 시간복잡도 좌우된다고 볼 수 있으며, O(ElogE)의 시간 복잡도를 갖는다.

3. 프림 알고리즘 (Prim's Algorithm)
3.1 Prim's Algorithm의 과정
0) 정점을 기준으로 MST를 찾아가므로, 각 정점에 연결된 간선 위주로 정보를 재구성
1) 방문한 노드를 방문된 노드 집합(visited_nodes)에 삽입
2) 선택된 노드에 연결된 간선들을 간선 리스트(candidate_edge_list, priority queue)에 삽입
3) 2의 간선 리스트에서 최소 가중치를 가지는 간선부터 추출하여 아래 작업 수행
3-1) 해당 간선에 연결된 인접 정점이 '방문된 노드 집합'에 있다면, skip (cycle발생X)
3-2) 없다면, 해당 간선을 MST(mst_list)에 삽입
-> 선택된 간선의 인접 정점의 간선들 중, 방문된 노드 집합(visited_nodes)에 없는 노드와 연결된 간선만 candidate_edge_list에 삽입
4) 3에서 선택된 간선은 candidate_edge_list에서 제거
3.2 Prim's Algorithm의 성능
앞서 정리한 프림 알고리즘의 과정 중 가장 핵심적인 부분은 "우선순위 큐"를 활용하여 다음에 방문할 "간선 리스트"를 찾아가는 과정이다. 일반적인 상황, 그리고 자바에선 우선순위 큐를 "힙" 자료구조를 활용하여 구현하므로 성능은 O(ElogE) 시간복잡도를 갖는다.
3.3 개선된 Prim's Algorithm : 노드에 우선순위 큐를 적용하자
Prim's Algorithm은 현재 방문한 노드를 중심으로 연결된 간선을 Priority Queue에서 정렬하여, 우선순위가 가장 빠른 간선으로 연결된 노드를 방문하여 MST를 찾아간다. 개선된 Prim's Algorithm은 간선이 아닌 노드에 focus를 둔다. 즉 다음에 방문할 노드를 간선이 아닌, 노드를 통해서 찾는다는 것이다.
code-level로 설명해볼까. Prim's Algorithm은 다음에 방문할 노드를 찾을 때 사용하는 대기 리스트를 Priority Queue로 구현하고, 이에 간선을 저장한다. 하지만 개선된 Prim's Algorithm은 대기 리스트를 Priority Queue로 구현하는 것은 동일하나, 노드를 보관한다.
<노드: 가중치 값>으로 구성된 map을 Priority Queue에 보관하고, 우선순위에 따라 가중치가 가장 작은 노드를 poll하여 다음 방문 노드로 지정한다. 모든 노드에 대한 가중치 값을 무한대로 초기화해두고, 현재 방문한 노드와 연결된 노드만 가중치 값을 update해둔다면 다음에 poll할 대상은 우선순위에 따라 가중치 값이 새롭게 update된 노드들이 될 것이다.
Prim's Algorithm은 "우선순위 큐"를 활용하여 다음에 방문할 "간선 리스트"를 찾아가는 과정이 성능에 가장 많은 영향을 준다고 했는데, 그래프는 간선보다 노드의 수가 적기 때문에 간선을 노드로 바꿔 성능을 개선하고자 한 알고리즘이다.
1. Priority Queue에서 Poll한 노드를 MST에 추가하고, (이 때 해당 노드와 연결된 from Node 정보가 필요하기에 Map이 필요)
2. 1에서 방문한 노드와 연결된 to Node를 모두 찾아, to Node에 대한 가중치 값이 Priority Queue에 저장된 가중치 값보다 작을 경우 <노드:가중치 값>을 update한다. (이 때 to Node에 대한 from Node(1에서 방문한 노드)를 함께 update)
3. Priority Queue에 남아있는 데이터가 없을 때까지 2의 작업이 끝나면 다시 1로 돌아가 작업을 반복한다.
3.4 개선된 Prim's Algorithm의 성능
개선된 Prim's Algorithm은 크게
1. Node의 수 만큼 방문할 노드 정보를 갖는 Priority Queue와 from Node정보를 갖는 Map 초기화 작업
2. Priority Queue에서 poll하여 MST구성
3. poll한 Node에 대해 Priority Queue update
세 가지의 과정을 갖는다.
1번은 노드의 수 만큼 작업하므로 O(V), 2번은 노드의 수만큼 Priority Queue에서 heap 정렬을 하여 poll하므로 O(VlogV)의 시간 복잡도를 갖는다. 3번은 최대 간선의 수 만큼 Priority Queue의 heap구조를 변경해야하므로 O(ElogV)의 시간이 소요된다.
따라서 O(V+VlogV+ElogV)이므로 간략하게 O(ElogV)로 표현할 수 있다.
'CS Engineering. > ALGORITHM' 카테고리의 다른 글
| 쓰이는 알고리즘 - 우선순위 큐(Heap)의 임의 요소 삭제에 관한 Idea (0) | 2021.03.17 |
|---|---|
| 쓰이는 알고리즘 - 그래프 알고리즘 기초(BFS, DFS, 최단경로 알고리즘, 백트래킹) (0) | 2021.02.24 |
| 쓰이는 알고리즘 - Recursive Call (재귀 호출) 언제 쓸까? (0) | 2021.01.27 |
| 쓰이는 자료구조 - Tree, Heap (Hash와 Tree의 성능비교 포함) (0) | 2021.01.26 |
| 쓰이는 자료구조 - Hash Table (1) | 2021.01.25 |