
1. Tree가 뭐에요?
- Node(이파리)와 Branch(가지)를 이용해서 원형 사이클 관계를 이루지 않도록 계층적(나무와 닮음)으로 구성한 데이터 구조
- 대표적으로 이진 트리의 구조로 자료 탐색 알고리즘 구현을 위해 사용되어진다.
- Node: 트리에서 데이터를 저장하는 구성 요소
- Branch: 트리와 트리를 연결하는 요소. 결국 하나의 Node에는 data와 다음 Node에 대한 link값을 가진다.
- Root Node: 최상위 노드
- Terminal Node(Leaf Node): Child Node가 하나도 없는 노드
- Sibling: 동일한 Parent Node를 가진 노드
- Level: 트리의 층 수
- Depth: 트리에서 Node가 가질 수 있는 최대 Level
- Sibling: 동일한 Parent Node를 가진 노드
- 이진 트리(Binary Tree): 최대 2개의 Child Node를 가지는 트리(= 최대 branch가 2)


2. Tree, 어떻게 활용될까?
앞서 말했듯, 트리 중 대표적인 "이진 트리"를 활용하여 탐색/정렬 알고리즘에서 활용된다. 왜, 탐색 알고리즘에서 효율적일까? 스무고개를 생각해볼까. 한 가지의 질문을 던질 때 마다 예/아니오 로 대답하여 정답 추론에 가까워진다. 이진 트리도 이와 유사하다. Root Node부터 시작해서 원하는 데이터를 찾기까지 예/아니오(크다/작다) 의 질문을 통해 빠른 자료 탐색을 할 수 있다.
- 이진 탐색 트리: 해당 노드보다 작으면 왼쪽 노드, 크면 오른쪽 노드에 자료를 저장하는 이진 트리
3. BST, 성능은?
depth를 h 그리고 노드의 개수를 n이라고 하면,
O(h) = O(logn) [h=logn]
* 빅오 표기법에서 log는 한번 실행할 때 마다, 실행할 수도 있는 명령의 갯수를 절반 줄인다는 의미에서 밑이 2이다.
* 균형잡힌 이진트리일 경우 O(logn)이지만, 트리가 한쪽 방향으로 치우쳐 있을 경우 O(n)이므로 균형잡히게끔 최적화작업이 필요하다.
4. Hash Table도 탐색 시 용이하다고 했는데, 성능 상 다른점이 있을까요?
- Hash와 BST의 가장 큰 차이점은 "정렬"이다. BST의 경우 값의 크기에 따라 삽입/삭제 시 마다 정렬이 이루어지지만, Hash의 경우 그렇지 않다.
- "탐색"의 경우, Hash는 Key값에 따라 저장된 위치를 찾기 때문에 O(1)의 일정한 탐색 성능을 보이지만, BST는 평균 O(logn) 최악의 경우 O(n)의 성능을 제공한다.
- 따라서 대부분의 작업에서 HashMap이 TreeMap보다 훨씬 빠르나, 키 값을 일정 수준으로 iterate하려한다면 TreeMap이 더 좋다.
- 입력 순서가 의미있다면 LinkedHashMap을 사용하면 된다(Link를 통해 입력 순서를 추가적으로 관리하는 HashMap). 하지만, 최악의 경우 O(n)성능을 보일 수 있으므로 많은 데이터 입력은 지양하는 것이 좋다.
5. Tree, 어떻게 사용할까?
- Java에선 TreeSet / TreeMap을 기본 라이브러리에서 제공하고 있다.
// String type의 데이터를 저장하는 BST
TreeSet<String> tree = new TreeSet<>();
// tree에 데이터 추가
tree.add("abc");
// tree에서 특정 조건에 맞는 범위의 sub tree 반환
// from은 포함, to는 미포함
tree.subSet(from, to);
// tree에서 최솟값, 최댓값 반환
tree.first();
tree.last();
// 최솟값/최댓값 반환 후 트리에서 삭제
tree.pollFirst();
tree.pollLast();
// 제공된 값보다 OO한 값 중 가장 OO한 값
tree.lower(arg); // 작은 값 중, 가장 큰 값(인자 제외)
tree.higher(arg); // 큰 값 중, 가장 작은 값(인자 제외)
tree.floor(arg); // 작은 값 중, 가장 큰 값(인자 포함)
tree.ceiling(arg); // 큰 값 중, 가장 작은 값(인자 포함)
// Tree는 비교연산이 가능해야하므로, comparator를 구현한 객체 type을 저장할 수 있다.
TreeSet<TestObject> treeSet = new TreeSet<>();
class TestObject implements Comparator<Object>{
@Override
public int compare(Object o1, Object o2){
}
}
* 근데, Set과 Map의 차이점은 뭐에요?
이전 포스팅에서 Hash에 다루면서 Map구조를 잠깐 봤었는데, Set은 값만 저장한다면 Map은 Key와 Value를 짝지은 Entry를 저장하는 자료구조이다.
6. Tree의 연장선, Heap
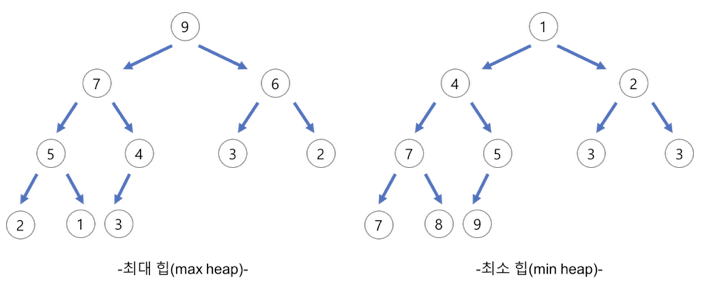
- Heap: 데이터에서 최댓값과 최솟값을 빠르게 찾기 위해 고안된 완전 이진 트리(CBT)
* CBT: 노드 삽입 시 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
6-1. Heap의 목적
- 배열에서 최댓값과 최솟값을 찾으려면 O(n)의 성능을 가진다.
- 힙에 데이터를 저장하면, 삽입/삭제 시 O(logn)의 성능을 가진다.
- 따라서 우선순위 큐와 같이 최댓값/최솟값을 빠르게 찾아야하는 자료구조 및 알고리즘에서 활용된다.
6-2. Heap의 구조
- 목적에 따라 Max Heap(최댓값 빠르게 구하기)과 Min Heap(최솟값 빠르게 구하기)으로 분류할 수 있다.
- 모든 노드는 자신보다 작거나 같은 값을 자식노드로 가질 수 있다. (Min Heap은 반대)
6-3. BST와의 차이점
- "자식 노드의 조건" 측면에서 가장 뚜렷한 차이를 보인다.
- BST는 Left Child는 작은 값, Right Child는 큰 값을 가지는 반면 Heap의 자식 노드의 조건은 "작거나 같다" 가 전부이다.(Max Heap의 경우)
- 오로지 최대/최소값 검색이 목적이라면 heap, 자료 탐색 혹은 정렬이 목적이라면 BST가 적합하다.
- 완전 이진 트리라는 구성을 갖춰야하나, BST에 비해서 삽입/삭제 과정이 간단하다.
- 일반적으로 Tree는 Linked List로 구현되나, CBT는 배열로 구현하는 것이 효율적이다. (index를 통해 삽입 위치 찾기가 용이)
6-4. 삽입과 삭제
- 삽입
CBT라는 조건으로 인해 빈 공간을 가지면 안되기 때문에 제일 마지막 공간에 값을 삽입한 후, 부모노드와 값을 비교해가며 위로 올라간다. 도장깨기랄까. 이러한 모습이 거품이 위로 올라가는 모양이라 하여 Bubble Up이라고 부른다.

- 삭제
삽입과 마찬가지로 빈 공간을 가지면 안되기 때문에 제일 마지막 노드를 root로 우선 올린다음, 자식노드와 값을 비교해가며 아래로 내려간다. 마치 좌천당하듯. 이러한 모습이 물방울이 떨어지는 모양이라하여 Trickle Down이라고 부른다.
삽입/삭제 시 root노드에서 값을 비교해나가는 과정이 최악의 경우 logn이기 때문에 성능은 O(logn)이다.
6-5. Heap을 정리해보면
힙 자체는 정렬된 것도 아니고 안된 것도 아닌 애매한 완전 이진 트리이나, 루트에는 항상 최댓값 혹은 최솟값을 가지기에 이를 통해 다양하게 활용될 수 있다.
가장 대표적인 것이 선형 자료 구조의 정렬 기법 중 하나인 'Heap Sort'이다. 한때 Java의 Array.prototype.sort에 채택된 방법. 현재는 Quick Sort를 채택하고 있다.
'CS Engineering. > ALGORITHM' 카테고리의 다른 글
| 쓰이는 알고리즘 - 그래프 기초(최소신장트리) (0) | 2021.03.17 |
|---|---|
| 쓰이는 알고리즘 - 그래프 알고리즘 기초(BFS, DFS, 최단경로 알고리즘, 백트래킹) (0) | 2021.02.24 |
| 쓰이는 알고리즘 - Recursive Call (재귀 호출) 언제 쓸까? (0) | 2021.01.27 |
| 쓰이는 자료구조 - Hash Table (1) | 2021.01.25 |
| 쓰이는 자료구조 - Array, Stack, Queue (0) | 2021.01.24 |